
课题组的一项最新研究将Thouless泵浦推进到了非线性范畴,并发现了分数阶Thouless泵浦现象。相关研究成果近日发表于《物理评论快报》。
在一些特定的周期系统里,波包的传输或者演化被发现是“拓扑”的,言下之意是:波包在横向跨越晶格时,其跨越的方向和位移仅仅决定于系统的某种全局特性——称之为“拓扑性”——而与其所在处系统的局部细节无关。在这种系统中,每经历一个演化周期T,波包在晶格内移动的距离R为R=CL, 其中L为晶格的一个周期的长度,C则为描写系统拓扑性的一个参数,称陈数。由于C只能取0,1,2,-1,-2等整数,所以,波包的此类移动是量子化的。该现象最早由物理学家David Thouless在1983年发现,后被称为“Thouless 泵浦”,又名“量子输运”(Quantum Transport)。 David Thouless因为在拓扑方面的工作获得了2016年诺贝尔物理学奖。值得说明的是,Thouless在该具有开创意义的工作中所考虑的物理系统是线性的,即描写系统的物理参数(如势函数,折射率)仅仅由系统本身决定,而与波函数的振幅等无关。
Thouless泵浦在很多物理系统中都得到了观察和实现。由于很多物理系统都可能具有非线性物理响应,一个很自然的问题是:非线性如何影响Thouless 泵浦?
课题组以自聚焦非线性响应为例,研究了非线性作用下波包在拓扑系统中的演化行为。他们发现,当波包的振幅比较小时(弱非线性范畴),波包的演化行为接近于线性系统下的行为,此时波包在演化过程中不断地扩散(但其质心位置仍然由R=CL精确地描述);随着波包振幅的增加,自聚焦效应不断增强,达到一定的阈值之后,非线性效应平衡了波包的扩散效应,一个稳定的波包——孤子就形成了。有趣的是,尽管此时波包作为一个稳定的整体在晶格中不断跨越,但其位置依然由R=CL精确描述 (图1(a)),即非线性仅仅起到了将波局域住的作用,但对其质心的位移并无任何影响。
继续增加波包的振幅会如何?研究者发现孤子的移动方向反转了(从向左传输变成了向右传输), 而移动距离也发生了变化:变成了线性情况的1/3(图1(b))!为什么?这是因为在这个阶段,非线性不仅仅起到了局域波包、形成孤子的作用,还耦合了各个能带,将前三个能带都均匀地激发出来可。因此,波包的传输由该三个激发带的平均拓扑陈数决定,即R=CeffL=1/3(C1+C2+C3)L。由于C1= C3=-1,C2=3,因此Ceff=1/3。即,Thouless 泵浦在较强非线性作用下,由于耦合了多个拓扑能带,出现了分数阶泵浦现象!
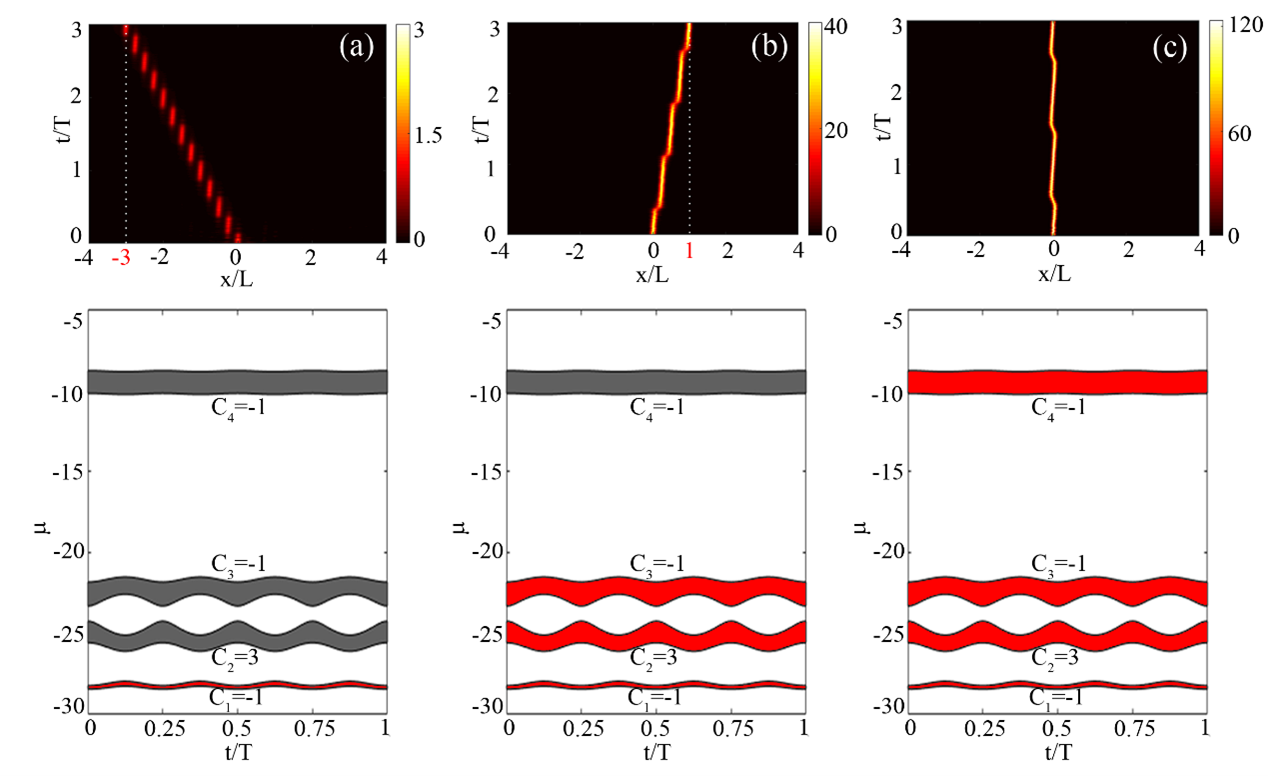
图1:非线性Thouless泵浦。随着非线性效应的增加,在三个演化周期T内,波包的演化先后经历: (a) 向左移动3个周期L(此时最低能带被激发,C1=-1), (b)向右移动1个周期L(此时前三个能带被激发,C1=-1,C2=3,C3=-1,即有效陈数Ceff=1/3, 对应分数阶泵浦), (c) 移动被“冻结”(此时,前四个能带被激发,C1=-1,C2=3,C3=-1,C4=-1,即有效陈数Ceff=0, 对应泵浦的非线性冻结)。
进一步增强波包的振幅又会如何?研究者发现,波包的移动最终归于“冻结”。这是因为更多的能带在非线性的作用下参与进来,导致有效陈数Ceff=1/4(C1+C2+C3+ C4)=0(图1c)。不过,有趣的是,此时的孤子尽管没有宏观上的定向移动,但出现了在原地不断“抖动”的现象,反映了相关激发能带之间的耦合和竞争。
非线性Thouless泵浦的研究发现意味着,通过控制波包的振幅这一个可调参数,就可以控制孤子波的移动方向和移动距离。这一研究从理论上将孤子的动力学行为和系统的拓扑性联系了起来,也为各类波(物质波,光波,声波等)定向移动的控制提供了一种新的调控手段。
相关论文信息:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.154101




