Hubbard模型是凝聚态物理中最基本的模型之一，它在强关联多电子体系研究中的地位类似于统计物理中的Ising模型，生物研究中的果蝇。强关联多电子体系中的众多奇异物态，特别是铜氧化物中的高温超导电性与它密切相关。目前虽然距离Hubbard模型的提出已经超过半个世纪，但由于求解强关联多体问题存在的普遍困难，关于二维Hubbard模型的性质仍然存在很大争议。虽然如此，求解Hubbard模型的尝试促进了众多高效数值方法的提出。这些方法对于研究强关联多体问题至关重要。

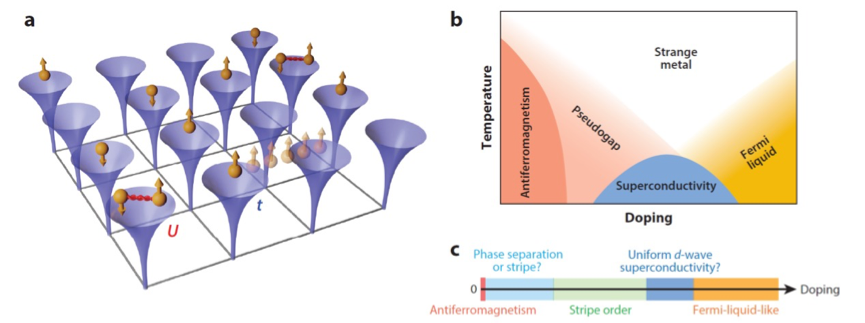
图 1. a, 二维Hubbard模型的图示。b(c), 二维Hubbard模型在有限温度（零温）的可能相图。

beat365中文版官方网站beat365中文版官方网站秦明普长期专注于Hubbard模型的研究以及相关数值方法的发展。最近他与来自于Max-Planck-Institut für Festkörperforschung的Thomas Schäfer，Universität Tübingen的Sabine Andergassen，University of Amsterdam的Philippe Corboz, 和University of Michigan的Emanuel Gull应邀为Annual Review of Condensed Matter Physics杂志撰写了标题为 “The Hubbard Model: A Computational Perspective”的综述文章。该文详细地总结了过去十多年在Hubbard模型研究中利用不同数值方法得到的进展，澄清了在Hubbard模型研究中的一些争议，特别是掺杂Hubbard模型中条纹相的确认。同时也指出了在Hubbard模型中有待解决的问题，如高温超导态可能出现的参数范围以及超导态和条纹相之间的关系。最后该文也强调了发展更高效更准确的方法对于最终求解Hubbard模型以至最终揭示高温超导机理的重要性。

原文链接：

https://www.annualreviews.org/doi/10.1146/annurev-conmatphys-090921-033948